In a previous blog post, we outlined some of the ways to improve EFDC+ model simulation efficiency to reduce the model runtimes. Specifically, the post addressed model timing and stability issues, as these are critical for many modeling applications. In this post, we continue this theme, focusing on the limits to model time steps and some suggestions for modifications to the model to increase efficiency.
Limitations on model time step
The overall model time step is based on the minimum time step considering all of the cells in the model. For example, if you have a model with 10 cells, and 9 of them can be run with a simulation time step of 20 seconds, but the remaining 1 cell requires a time step of 1 second, then the entire model must be run with a time step of 1 second.
Therefore, if a model is running slowly due to one cell limiting the overall time step, often some slight adjustments to those cells can result in significant improvements in the overall model efficiency. There are several tools in EFDC+ and EE to help the users in this process and make what otherwise might be a tedious and time-consuming task much easier and faster for the user, as described below.
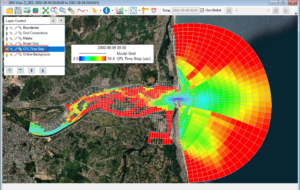
1. CFL Time Step: Before simulation results have even been obtained, EE allows the user to view initial predictions of the Courant–Friedrichs–Lewy (CFL) minimum time step, as shown in Figure 1. The CFL condition is necessary condition for convergence when solving partial differential equations. In the case of the CFL minimum time step, the user will see the suggested CFL time step for each cell necessary to ensure closure of the hydrodynamic equations.
For example, the Figure 1 shows areas of smallest time steps are near the mouth of the estuary. Depending upon the model objectives, you may want to reduce the cell resolution and/or adjust the model bathymetry to increase the CFL Time step.
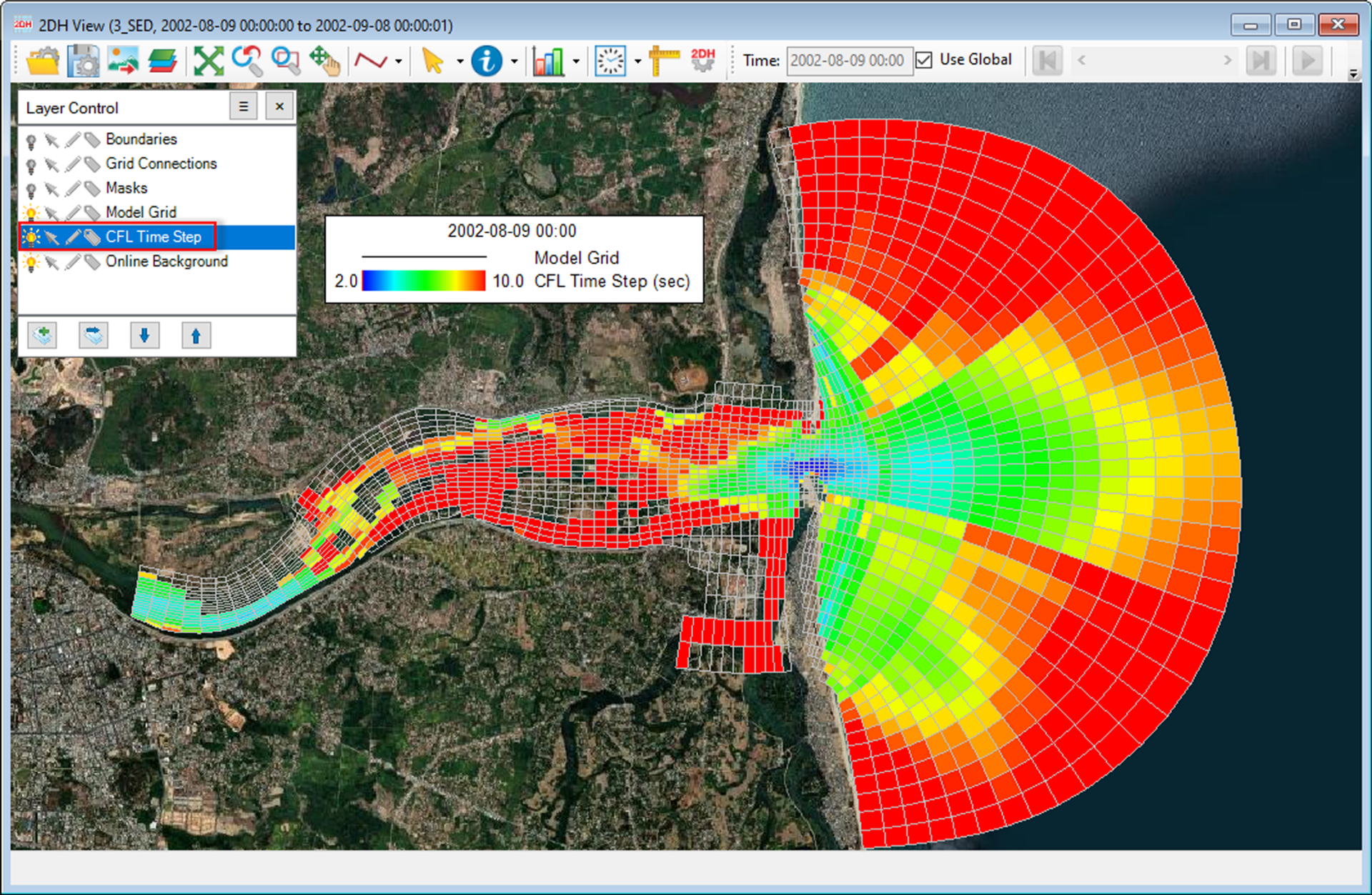
2. Courant Number: After even a few brief time snapshots from the model output, the Courant number can also be inspected, as shown in Figure 2. The Courant number is a dimensionless value representing the time a particle stays in one cell of the mesh. The information available through the Courant number and the CFL Time step can be used together to focus on cells that may be the cause for the smaller model time step and greater model run time.
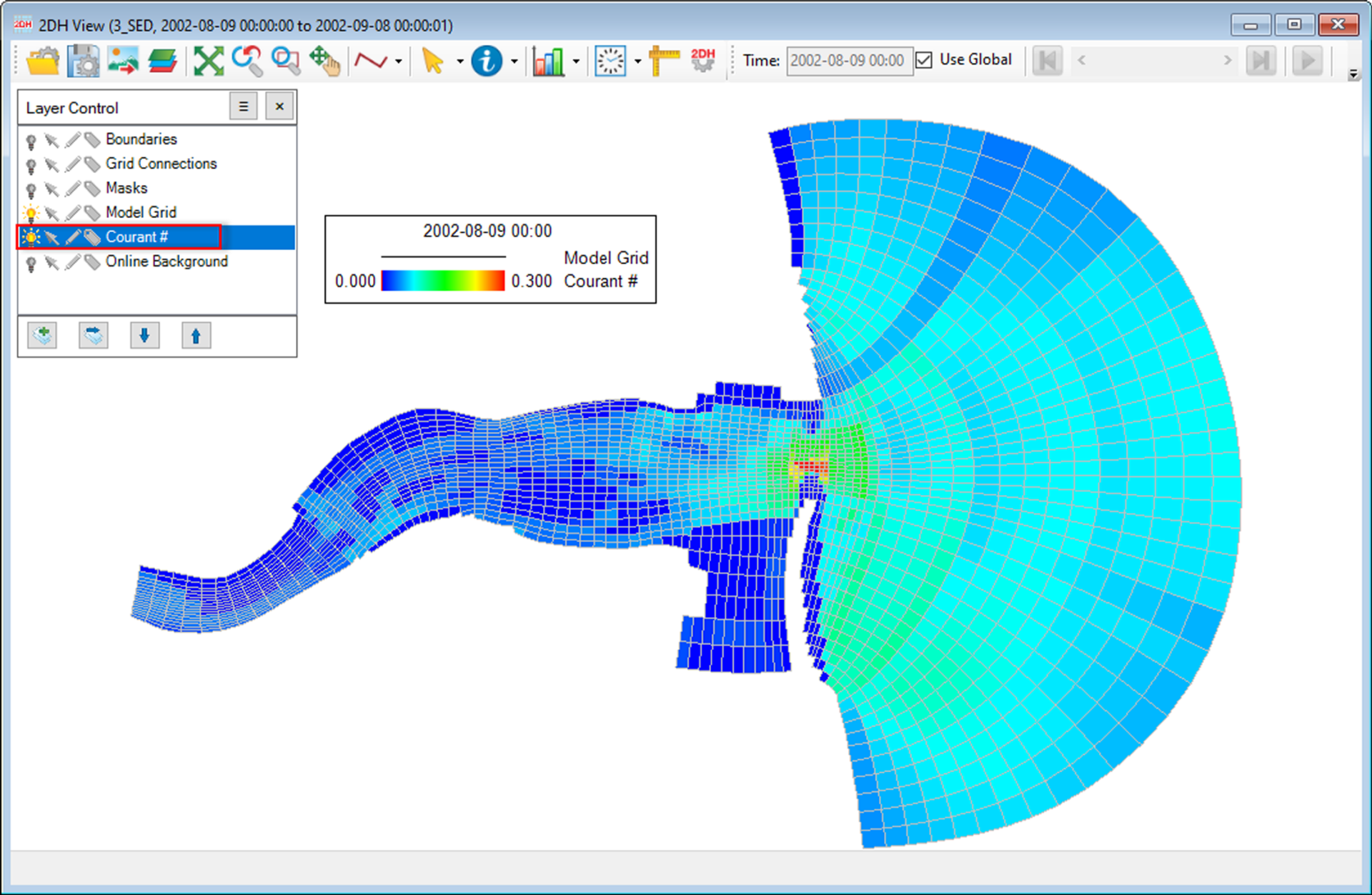
3. While running a model with EFDC+ using a two time level solution, the user receives immediate feedback on the cell (L index), which imposes a limitation on the maximum time step of the entire model. For most models, this LMIN value doesn’t usually change that quickly unless the model is ramping up. However, once the model has found the approximate maximum time step, based on the user-specified initial and maximum time step, ramp-up loops, and growth steps, this LMIN value will generally be the L index of only a small number of cells which are most problematic for further growth of the time step. Paying close attention to the LMIN column while the model is warming up in an initial simulation can provide some immediate clues as to where to begin your investigation of individual cells that may be potential candidates for adjustment and help us improve our model efficiency.
Theory behind mathematic constraints
EFDC+ is a finite-difference numerical model which uses an explicit solution based on the upwind/upstream differencing approach (two time level solution) or a central differencing approach (optional with the three time level solution). There are well defined mathematical constraints on the model time step for these equations in EFDC+, as there are for all such numerical models. We can determine these by looking at the several dimensionless coefficients. For a central differencing approach, these include the Reynolds Number, Courant Number, and Peclet Number (e.g., Daus et al., 1985):
Where,
v is the velocity (L/T),
L is the flow length (L),
D is mass diffusion coefficient (L²/T),
\delta \mathbf{x} is the cell discretization length (L), and
\delta \mathbf{t} is the time step (T).
The Peclet number is defined as the ratio of the rate of advection of a physical quantity by the flow to the rate of diffusion of the same quantity. For flows that are advection dominated (i.e., large Reynolds numbers), the Peclet number condition \left(P_e \leq 2\right) must be satisfied to ensure that oscillations do not persist in the model. Additionally, the Courant number condition requires that the timestep is less than or equal to unity \left(C \leq 1\right) Combining the Peclet and Courant number conditions, we get:
Advection dominated flows, however, can often result in conditions where it is difficult to satisfy the Peclet number criteria. When such conditions arise, it is possible to use the upstream/upwind differencing approach. Doing so, using similar conditions, produces:
Thus when using the upwind differencing scheme in advection-dominated systems, the stability time step is reduced, but there is no strict Peclet number effect.
In summary, the Reynolds number comes from the physics of the problem. The Peclet number looks like a mesh Reynolds number, but its influence depends on the numerical method. Central differencing has been shown to produce spurious oscillations (resulting in model instability) unless the \left(P_e \leq 2\right). However, P_e has no direct impact on the time step limit. With the upstream/upwind difference scheme, the influence of the Peclet number is to decrease the time step. For this reason, to support a forward difference, two time level algorithm in EFDC+ requires the upstream/upwind differencing approach. The three time level approach can use either the central or upstream/upwind differencing approach.
Using the properties of the cell, the velocity of flows in the model, and other physical parameters, these conditions can be used to better understand where/ which cell the model is struggling to maintain stability.
Reference:
Daus, A.D., Frind, E.O., Sudicky, E.A., 1985. Comparative error analysis in finite element formulations of the advection–dispersion equation. Adv. Water Resour. 8, 86-95
What you can do to improve efficiency
- Re-evaluate and improve boundary and initial conditions: Any mismatch between the boundary conditions or initial conditions or rapid dynamic changes in the boundary conditions can result in model instability. For example, a coastal model may have a fixed water level of 5 m in the open ocean, but the open boundary varies between 15 and 20 m. Or inflows into a river may vary too rapidly due to bad data. It is always a good idea to inspect boundary condition inputs at various resolutions to evaluate the appropriateness of short- and long-term changes based on your understanding of the system.
- Modify cell properties (i.e., bottom elevation, aspect ratio, etc.): EE includes powerful graphical tools to quickly identify cell properties, search for cells, and modify cell properties such as direction without changing input files directly. Grid+ can import model grids already used for previous EFDC+ models, modify them, and output the necessary files to support further model development (Caution: modifying the model cell indices will break boundary conditions or cause them to appear in incorrect locations). EE has a wide range of operations, such as copying/pasting, and modifying cell properties, importing shapefiles, manually selecting cells to perform operations on, or applying data from other sources directly (i.e., an XYZ file for bathymetry). These operations can be used to adjust cell properties and potentially improve the ability of the model to make predictions in that area without violating the necessary Courant condition.
- Adjust time step configuration: After adjusting cell properties, ensuring initial and model boundary condition consistency, and modifying any other model parameters, creating some new model runs using different timing configurations can be helpful to see how much of an effect the changes made to the grid/boundary/initial conditions had. Sometimes further adjustment or evaluation might be required. Cells adjacent to those causing the model to slow down can also be a source of problems if, for example, the cells representing the cross-section of the river are unnecessarily constricted, or the channel narrows in an extreme or unrealistic manner. Flow may be forced into a single cell, causing velocities to increase dramatically.
- Activating Wetting and Drying: Cells that may wet and dry too frequently can also contribute to model slow-downs. If such issues are encountered, EFDC+ includes various options for modifying wetting and drying behavior. These parameters include the ‘Wet Step’ (i.e., the number of time steps between checking the wet/dry condition) or the ‘Dry Depth’ (i.e., the depth below which a cell is considered dry). Note that if wetting and drying is not activated, all cells will be assumed wet, with at least the minimum depth specified by the ‘Dry Depth.’ This can result in undue computational burden since the model will cycle through these cells at every time step to ensure the mass balance remains closed in these areas.
EE provides you with enough information to visualize and analyze important model metrics that you can use to improve your model performance. Download any of the test or demo models available on our website and try them out.
Happy Modeling,